每当介绍相位噪声测试方案时,都会提到时间抖动,经常提到二者都是表征信号短期频率稳定度的参数,而且是频域和时域相对应的参数。正如题目所示,相位噪声与时间抖动有着一定的关系,那么相噪是与哪种类型的抖动相对应,彼此之间又有着怎样的数学关系,这些疑问都将在文中找到答案。
1. 相位噪声与时间抖动概述
相位噪声通常是针对CW信号而言的,是表征信号频谱纯度的非常重要的参数,衡量了信号频率的短期稳定度。相位噪声是频域的参数,在时域还有一个与之对应的参数——随机抖动,二者之间存在一定的数学关系,可以相互转换。
在前面关于相位噪声测试的文章中,给出了IEEE早期关于相噪的定义,同样的,关于时间抖动,SONET规范也给出了相应的定义:
“Jitter is defined as the short-term variations of a digital signal’s significant instants from their ideal positions in time”.
抖动定义中给出了三个要素:
(1) significant instants,通常是指信号的上升沿或者下降沿;(2) ideal positions in time,这是指信号上升沿或下降沿在时间维度上的理想位置;
(3) short-term variations,信号实际上升沿或下降沿相对于理想位置时间偏移的短期波动。
虽然定义中只提到了数字信号,但实际上具有普遍适用性,当然对于CW信号也是适用的。
上述定义所给出的是一种综合性抖动,按照不同的原因机制,又可以分解为多种不同的抖动分量,包括:随机抖动,周期性抖动,数据相关抖动,占空比失真等。
CW信号可以理解为一种特殊的数字码流信号,理论上只有随机抖动和周期性抖动这两种分量。随机抖动是由宽带噪声引起的,周期性抖动是由串扰引起的,从产生机制上讲,都相当于对信号进行了调频或者调相。
高端的频谱仪及专业的相噪测试设备,除了能够给出相位噪声,还可以测试载波附近的spur。根据产生的机制可以判定,相位噪声是与随机抖动相对应的,spur是与周期性抖动相对应的。
下文主要聚焦在相噪与随机抖动的关系,后面所提到的抖动,除非特别说明,否则一律视为随机抖动。
2. 相位噪声与时间抖动有何关系?
理想的CW信号用公式可以表示为
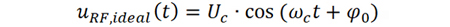
相位噪声可以理解为宽带随机噪声对CW信号的相位调制,因此,CW信号的频谱具有对称的左右两个边带。
从相位调制的角度看,经宽带随机噪声u(t) 调制后,已调信号可以表示为
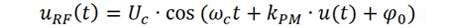
式中,kPM为调相比例系数,u(t) 为宽带随机信号,通常可以视为白噪声信号,相当于由无数个点频信号叠加而成。
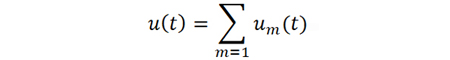
对于u(t) 中包含的任意频点ꞷm,对应的调制信号表达式为
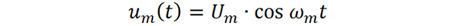
下面以频率为ꞷm 的信号作为调制信号,从数学的角度推导单边带相位噪声与时间抖动的关系。
对射频载波调相后,已调信号的表达式为
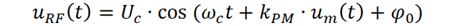
由调制信号引起的载波信号的瞬时相位定义为
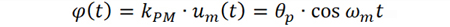
通常称θp 为调相因子,表征了载波信号相位波动的最大偏移,单位为弧度rad.,其表达式为
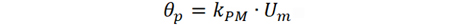
因此,已调信号又可以写为

将上式展开为
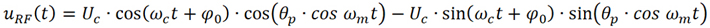
因宽带噪声幅度非常小,对载波信号进行相位调制造成的相位偏移也是非常小的,通常θp<<1,则存在如下近似关系:
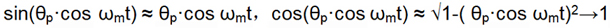
上式可进一步写为

理论上,如果使用单频点信号作为调制信号对射频载波进行相位调制,已调信号可以展开为第一类贝塞尔函数,从展开式可以看出,频谱分量非常丰富,而且关于载波频率左右对称。而上面的公式表明,却只有载波、左右边带三个频率分量,这正是因为上面做了一些数学近似。
以右边带为例,其信号功率为
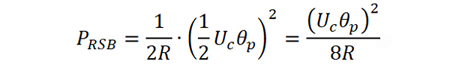
载波信号功率为
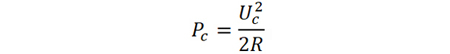
则在频偏fm=ꞷm/2π 处的单边带相位噪声为
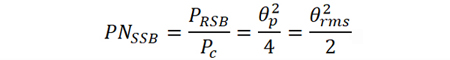
式中,θrms为载波信号相位波动的有效值。该公式具有普遍适用性,适用于任意频偏。
相位噪声表征了某一频偏处的单边带相对噪声功率谱密度,由上式可知,θ2rms表征了双边带相对噪声功率谱密度。
上面是以宽带随机噪声中的任意单频点信号作为调制信号为例,简要描述了相位噪声的形成,而宽带噪声包含无数个单频点信号,对载波进行相位调制后,那么从频谱上看,同样可以得到左右对称的两个边带,而且左右边带的频谱是连续的。
随机抖动与相位噪声有什么关系呢?
时间抖动就是指载波信号上升沿或者下降沿在时间轴上的短期波动,随机抖动是由于宽带噪声引起的边沿无规则随机波动,这与相位噪声是一一对应的,边沿的波动是各个频偏处相噪的综合体现。载波边沿的随机波动,存在一个波动范围,从概率密度上讲,基本服从高斯分布,通常采用标准差表征随机抖动,这也是随机抖动的有效值,也是通常要测试的参数。
时间抖动引起了相位的波动,只要确定了相位波动的量,那么也就确定了时间抖动。
将各个频偏处的相位噪声求和并进一步变换可得
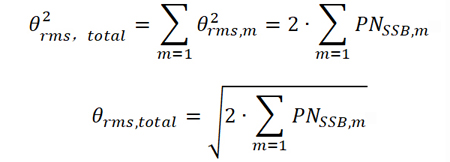
由于相位噪声的边带是连续的,因此,上式可以用积分表示
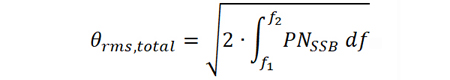
当然,测试设备是没有办法进行积分的,只能对离散的测试数据进行求和来模拟积分的效果。
θrms,total 即为由总体的相位噪声引起的相位波动,结合载波频率并运用如下公式便可以计算出对应的时间抖动
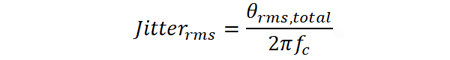
值得一提的是,上述公式中的相位噪声不是对数值,而是线性值!而且,根据相位噪声计算得到的抖动为随机抖动,换言之,随机抖动与相位噪声是一一对应的。
3. 如何测试时间抖动?
从目前看,关注时间抖动的信号主要分为两类:快沿信号和CW信号。前者通常是指在高速串行总线通信中的比特流信号及其时钟信号,这类信号普遍具有非常快的边沿,频谱分量较为丰富。后者主要是指诸如射频载波、晶振信号等单频点信号,这类信号频谱相对单一。
使用示波器是测试时间抖动最直接的方法,可以直接测试抖动,而不需要由相位噪声推导而来,对于上述两类信号都是适用的。尤其是对于快沿信号,不仅要测试各种抖动分量,还要测试幅度、边沿时间以及眼图等信号特征参数,必须要使用示波器进行测试。
对于CW信号,基本上只关注随机抖动,如果给出了抖动的指标要求,一定会给出对应的是哪个频偏范围。中高端示波器可以直接测试随机抖动,而且支持设定积分频偏范围,观测该频偏范围内的总随机抖动。但缺点是,示波器自身的抖动噪底往往较大,如果CW信号自身的随机抖动与示波器抖动噪底相当,那么就无法直接准确测试了。
如前所述,由相位噪声可以推导出随机抖动,那么就可以先测试相位噪声,然后再根据公式计算出随机抖动。通过配置自动相噪测试选件,中高端频谱仪测试相噪和抖动更加方便。而且单纯从随机抖动的测试能力而言,频谱仪自身的抖动噪底也好很多,如果超出了频谱仪的测试能力,还可以选择测试相噪的“专家级”设备——信号源分析仪,相噪测试能力更强。优点很明显,但缺点也很明显,这些频域设备只能测试频域相关参数,却无法进行时域相关测试!
无论是使用示波器直接测试随机抖动,还是使用频谱仪等设备先测试相噪、再计算随机抖动,整个测试都是非常简单、智能的。那么,应该如何选择呢?关键还是取决于仪表自身的测试能力和功能是否满足需求!
以上便是要给大家分享的内容,希望对大家有所帮助~~
小文虽短但不乏精华,希望大家持续关注“微波射频网”,后续精彩不断~

 粤公网安备 44030902003195号
粤公网安备 44030902003195号